20220117 동적계획법 - LCS
동적계획법에 대하여 알고싶다면 여기
| 동적계획법을 통한 문제 해결방법
동적계획법으로 문제를 해결하는 방법을 다시 짚어보자면,
1. 해를 분석하여 부문제로 분할한다.
2. 부문제의 해로 큰 문제의 해를 표현한다. (큰 문제의 해는 부문제의 해에 대한 점화식으로 보통 표현된다)
여기서 부문제의 해와 큰 문제의 해들은 모두 DP table 에 저장되어 있다.
3. 적당한 순서대로 DP table을 채운다.
4. table을 통해서 해를 계산하고 알고리즘의 정확성을 증명한다.
| LCS 문제란
가장 긴 길이의 공통 부문자열을 찾고 이의 길이를 반환하는 문제
즉, 모든 문자열의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제
*부문자열이란 : 부분 수열
ex. A를 지우면 남는 부문자열 : B, ABC, ABC ..
X = ABCBDAB
Y = BDCABA
라고 가정하면,
길이가 1인 경우는 A,B,C,D
길이가 2인 경우는 AB, DA..
길이가 4인 경우는 BDAB, BCAB
길이가 5인 경우는 없음. 따라서 답은 BDAB, BCAB
| 동적 계획법으로 접근해보기
1. 두 문자열에 대하여 변수로 만들기
첫번째 문자열을 X로 두고, 문자열의 첫번째 문자를 x1, 두번째 문자를 x2, ... i번째 문자를 xi
두번째 문자열은 Y로 두고, 문자열의 첫번째 문자를 y1, 두번째 문자를 y2, ... j번째 문자를 yj 으로 두자.
또한 인자로 i,j를 넘긴다면 이는 xi와 yj의 LCS의 길이를 반환하는 LCS라는 함수를 생성한다고 가정하자.
2. case 1. xi = yj
만일 두 문자열의 가장 마지막 문자가 같다면 이를 LCS 에 포함시키는 것이 당연한 수순이다. (공통인 문자이기에)
여기서 마지막 문자열을 포함시키고 나면 그 앞 문자열에 대하여 LCS함수를 호출하면 된다. 따라서 xi = yj라면 LCS(i,j) = LCS(i-1,j-1)+1이 된다.
case 2. xi != yj
그러나 두 문자열의 가장 마지막 문자가 다르다면 LCS에 맨 마지막 문자를 포함시키지 않고, 첫번째 문자열의 맨 마지막 문자가 포함될 수도 있고, 되지 않을 수도 있으며 두번째 문자열의 맨 마지막 문자 역시도 포함될 수도 있고, 아닐 수도 있다. 따라서 xi != yj라면 LCS(i-1,j) 와 LCS(i,j-1) 중 더 큰 값을 갖는, 즉 길이가 더 긴 경우를 반환하면 된다.
3. DP table 2차원으로 생성한다.
DP table을 다음 사진과 같이 2차원으로 생성하여 LCS(7,6)에 최종 문자열의 길이가 담길 수 있도록 한다.
여기서, 각 문자열의 첫번째 인덱스에는 기본적으로 0을 넣도록 한다.

4. table의 바닥 조건을 설정
table의 바닥 조건을 설정해야 하는데 이는 각 문자열의 맨 처음인 0을 통해서 설정할 수 있다.
만일 LCS(0,j) 즉 X 문자열에는 아무것도 존재하지 않고 Y 문자열만 존재한다면 이에 대한 공통적인 부문자열의 길이는 모두 0이다. 따라서 DP table의 첫번째 행은 모두 0이 된다. 이는 반대로 LCS(i,0)에도 적용된다. 따라서 table의 첫번째 열 역시도 모두 0이다.
그렇다면 이제 테이블을 채워보자.

빨간색으로 표시된 부분을 구해야 한다고 가정해보자. 만일 빨간색으로 표시된 부분의 문자가 서로 같다면, 즉 범위의 맨 마지막 문자가 같다면 파란색 부분을 구하면 된다. (위에서 언급한 case 1과 같은 경우이다.) 만일 해당 부분의 문자가 서로 다르다면 초록색 부분을 구하면 된다. (위에서 언급한 case 2와 같은 경우이다.) 초록색 부분을 구하기 위해서는 한 행 위를 구해야 하고, 또 초록색의 한 행 위를 구하기 위해서는 또 다시 한 행위를 구해야 하고.. 이에 대한 반복이다. 따라서 table은 row by row 로 채워질 것임을 알 수 있다.
실제로 테이블의 일부를 채워보자면, 아래의 그림과 같다.
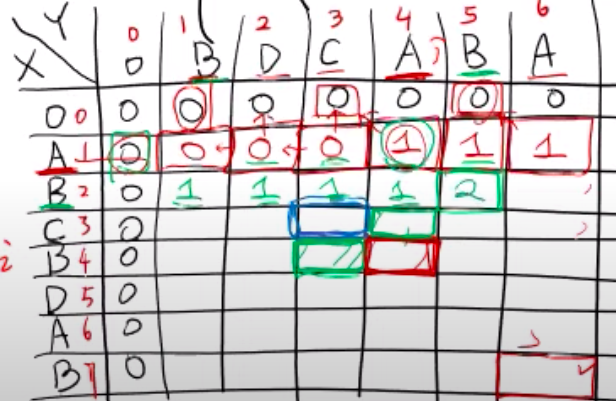
LCS[1][1]은 LCS(1,1)과 같다. 이는 A와 B로 서로 다르므로 LCS[0][1]과 LCS[1][0] 중에 더 큰 값을 택한다. 이는 0이므로 0이고,
LCS[1][4]를 구해보자면 이는 LCS(1,4)와 같다. 이는 A로 같으므로 case 2와 같기에 LCS[0][3]의 값에 1을 더하면 된다. 이는 0+1이므로 1이 된다.
| LCS 문자열 알아보기
그러나 여기서, LCS의 길이는 알아냈지만 (LCS[i][j]를 반환하면 알 수 있다) 어떤 문자열인지는 알아내지 못했다. 이는 table을 거꾸로 역추적 하면 알아낼 수 있다. LCS[i][j]를 시작점으로 두고, 해당 위치에 저장된 값이 어디에서 왔는지를 추적하다보면 LCS 문자열이 나온다.

1. LCS[7][6]의 문자열은 다르기에 LCS[6][6]이나 LCS[7][5]에서 온 것이다. 그 둘 중 더 큰 값에서 왔다는 표시로 위를 향하는 화살표를 표시하고 해당 값으로 이동한다.(여기서는 4로 값이 같으므로 어떤 위치로 이동하던 상관없다.)
2. 그 위에 있는 LCS[6][6]은 X와 Y의 문자가 A로 같으므로 LCS[5][5]에서 온 것이다. 따라서 대각선을 향하는 화살표를 표시하고 해당 위치로 이동한다. 여기서 같은 문자가 등장한 경우에는 이를 따로 표기해둔다.
이러한 과정을 반복하다보면, 사진에 따르면 LCS[2][1], LCS[3][3], LCS[4][5], LCS[6][6]이므로 BCBA이다.
| 소요시간
이중 for문을 통해서 테이블을 모두 채운다면, n*m이기에 O(nm)이지만 m이 n보다 작거나 같다면 O(n^2)이다. for문 내에서는 table을 채우기 위해서 몇가지의 연산만을 수행했기 때문에 상수시간이 걸린다.